高二数学《等差数列的前n项和》教学设计
11-01 11:08:11 | 浏览次数: 68918 次 | 栏目:数学教学设计
标签:数学教学设计,http://www.manfen6.com
高二数学《等差数列的前n项和》教学设计,



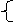







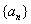











 TAG: 教学 高二数学
TAG: 教学 高二数学
是一个首项为
,公差为2的等差数列。
这个例题还给出了等差数列通项公式的一个求法.已知前n项和
,可求出通项
(n>1)
用这种数列的
来确定
的方法对于任何数列都是可行的,而且还要注意
不一定满足由
求出的通项表达式,所以最后要验证首项
是否满足已求出的
.
思考:结合例3,思考课本51页“探究”:一般地,如果一个数列
的前n项和为
其中p、q、r为常数,且p≠0,那么这个数列一定是等差数列吗?如果是,它的首项与公差分别是什么?
引导分析得出:观察等差数列两个前n项和公式
,和
,公式本身就不含常数项。
所以得到:如果一个数列前n项和公式是常数项为0,且关于n的二次型函数,则这个数列一定是等差数列.
例4 已知等差数列
的前n项和为
,求使得
最大的序号n的值.
分析:等差数列的前n项和公式可以写成
,所以
可以看成函数
当x=n时的函数值.另一方面,容易知道
关于n的图象是一条抛物线上的一些点.因此,我们可以利用二次函数来求n的值.
解:由题意知,等差数列
的公差为
- ·上一篇:《各具特色的民居》 趣闻故事
- ·下一篇:少儿英语游戏:单词接龙
《高二数学《等差数列的前n项和》教学设计》相关文章
- › 高二数学《算法初步》单元测试
- › 高二数学:函数专题介绍
- › 高二数学期末复习题
- › 高二数学理科复习题-椭圆
- › 高二数学复习卷
- › 高二数学学习心得体会总结
- › 高二数学复习八大法则
- › 高二数学《几何概型》单元测试
- › 高二数学《向量的线性运算》同步练习题
- › 高二数学《等差数列》教学设计
- › 高二数学《基本不等式》教学设计
- › 高二数学《分期付款问题的研究性学习》教学设计
- › 高二数学《定积分的概念》教案
- › 高二数学全册教案
- › 2016年高二数学暑假作业答案
- › 高二数学寒假复习题及答案
- 在百度中搜索相关文章:高二数学《等差数列的前n项和》教学设计
最新更新