高二数学《任意角的三角函数》教学设计
11-01 11:51:25 | 浏览次数: 50018 次 | 栏目:数学教学设计
标签:数学教学设计,http://www.manfen6.com
高二数学《任意角的三角函数》教学设计,
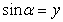


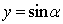




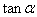
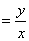
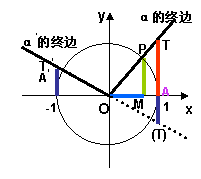

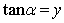






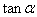
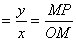
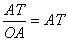 TAG: 教学 高二数学
TAG: 教学 高二数学
.取角
的终边与单位圆的交点为P,过点P作
轴的垂线,设垂足为M,则有向线段MP=
.(学生分析的同时,教师用几何画板演示)
请学生利用几何画板作出垂线段MP,并改变角的终边位置,观察终边在各个位置的情形,注意有向线段的方向和正弦值正负的对应.特别地,当角的终边在
轴上时,有向线段MP变成一个点,记数值为0.
这条与单位圆有关的有向线段MP叫做角
的正弦线.
2.思考:用哪条有向线段表示角
的余弦比较合适?并说明理由.
请学生用几何画板演示说明.
有向线段OM叫做角
的余弦线.
3.
如何用有向线段表示?
讨论焦点:
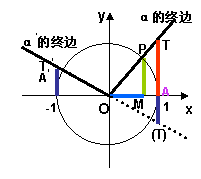
若令
=1, 则
=AT,但是第二、三象限角的终边上没有横坐标为1的点,若此时取
=-1的点T‘,tan
=-
=T‘A‘,有向线段的表示方法又不能统一.
引导观察:
当角的终边互为反向延长线时,它们的正切值有什么关系?
统一认识:
方案1:在象限角的终边或其反向延长线上取
=1的点T,则tan
=
=AT;
方案2:借助正弦线、余弦线以及相似三角形知识得到
=
上一页 [1] [2] [3] [4] [5] [6] 下一页
- ·上一篇:依依惜别的深情──读《再见了,亲人》有感
- ·下一篇:由“7+30=73”引发的思考
《高二数学《任意角的三角函数》教学设计》相关文章
- › 高二数学《算法初步》单元测试
- › 高二数学:函数专题介绍
- › 高二数学期末复习题
- › 高二数学理科复习题-椭圆
- › 高二数学复习卷
- › 高二数学学习心得体会总结
- › 高二数学复习八大法则
- › 高二数学《几何概型》单元测试
- › 高二数学《向量的线性运算》同步练习题
- › 高二数学《等差数列》教学设计
- › 高二数学《基本不等式》教学设计
- › 高二数学《分期付款问题的研究性学习》教学设计
- › 高二数学《定积分的概念》教案
- › 高二数学全册教案
- › 2016年高二数学暑假作业答案
- › 高二数学寒假复习题及答案
- 在百度中搜索相关文章:高二数学《任意角的三角函数》教学设计
最新更新