高二数学《等差数列》教学设计

11-01 11:56:30 | 浏览次数: 27018 次 | 栏目：数学教学设计

标签：数学教学设计,http://www.manfen6.com 高二数学《等差数列》教学设计,

　　③ 这个数列的第一项是18，第2项是15.5(=18-2.5)，第3项是13(=18-2.5×2)，第4项是10.5(=18-2.5×3)，第5项是8(=18-2.5×4)，第6项是5.5(=18-2.5×5)由此可以猜想得到这个数列的通项公式是

　　④ 这个数列的第一项是10072，第2项是10144(=10172+72)，第3项是10216(=10072+72×2)，第4项是10288(=10072+72×3)，第5项是10360(=10072+72×4)，由此可以猜想得到这个数列的通项公式是

　　⑵、那么，如果任意给了一个等差数列的首项

　　和公差d，它的通项公式是什么呢?

　　引导学生根据等差数列的定义进行归纳：

　　(n-1)个等式

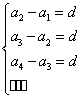
　　所以

　　……

　　思考：那么通项公式到底如何表达呢?

　　……

　　得出通项公式：由此我们可以猜想得出：以

　　为首项，d为公差的等差数列

　　的通项公式为：

　　也就是说，只要我们知道了等差数列的首项

　　和公差d，那么这个等差数列的通项

　　就可以表示出来了。

　　选讲：除此之外，还可以用迭加法和迭代法推导等差数列的通项公式：

　　(迭加法)：

　　是等差数列，所以

　　……

　　两边分别相加得

　　所以

　　(迭代法)：

　　是等差数列，则有

TAG: 教学高二数学