高一必修二《圆与方程》课堂练习
11-01 11:57:02 | 浏览次数: 54618 次 | 栏目:数学知识点总结
标签:数学知识点总结,http://www.manfen6.com
高一必修二《圆与方程》课堂练习,
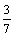
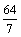
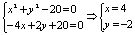
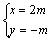



TAG: 课堂
(2)r2= D2+E2-4F=4(t+3)2+4(1-4t2)2-4(16t4+9)=-28t2+24t+4=-28(t-
)2+
,
21. 解:(1)曲线C的方程可化为:(x2+y2-20)+m(-4x+2y+20)=0,由
,
∴不论m取何值时,x=4, y=-2总适合曲线C的方程,即曲线C恒过定点(4, -2).
(2)D=-4m, E=2m, F=20m-20, D2+E2-4F=16m2+4m2-80m+80=20(m-2)2
∵m≠2, ∴(m-2)2>0, ∴D2+E2-4F>0, ∴曲线C是一个圆, 设圆心坐标为(x, y), 则由
消去m得x+2y=0, 即圆心在直线x+2y=0上.
(3)若曲线C与y轴相切,则m≠2,曲线C为圆,其半径r=
,
又圆心为(2m, -m),则
=|2m|,
.
- ·上一篇:2016四年级开心暑假答案
- ·下一篇:2016初一数学暑假乐园答案
《高一必修二《圆与方程》课堂练习》相关文章
- › 高一必修二《两条直线的平行与垂直》练习题
- › 高一必修二《直线的方程》练习题
- › 关于高一生物复习方法:高一必修复习提纲
- › 荆轲刺秦王(人教版高一必修)
- › 人教版高一必修4文言文阅读同步训练
- › 人教版高一必修一英语教案
- › 高一必修二《直线与方程》课堂练习
- › 高一必修二《圆与方程》课堂练习
- › 高一必修二《直线、平面、简单几何体》练习题
- › 高一必修一《直线与平面垂直的判定(一)》教案
- › 高一必修二《点到直线的距离》说课稿
- › 高一必修二《圆的标准方程》的说课稿
- › 北师大版高一必修二数学教案
- › 北师大版高一必修三数学教案
- › 牛津英语高一必修一教案
- › 高一必修一《圆的方程》教学设计
- 在百度中搜索相关文章:高一必修二《圆与方程》课堂练习
最新更新