高一必修二《直线、平面、简单几何体》练习题
11-01 11:57:02 | 浏览次数: 83818 次 | 栏目:数学知识点总结
标签:数学知识点总结,http://www.manfen6.com
高一必修二《直线、平面、简单几何体》练习题,
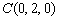
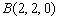

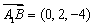
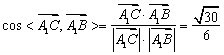

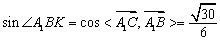
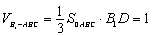




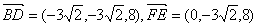



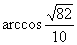
TAG: 练习题 平面 几何体
,
,∴
,
∴
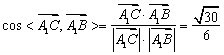
设A1C
平面BDE=K,由⑴可知,∠A1BK为A1B与平面BDE所成角,
∴
21.⑴在平面ABB1A1中,作B1D⊥AB,则B1D⊥平面ABC
∴∠B1BD为B1B与平面ABC所成角,∴∠B1BD=60?
又∵△ABB1和△ABC均为正三角形,∴D为AB中点,∴CD⊥AB,∴CB1⊥AB
⑵易得
⑶过D作DE⊥AB1,连CE,易证:CD⊥平面ABB1A1
由三垂线定理知:CE⊥AB1,∴∠CED为二面角C-AB1-B的平面角。
在Rt△CDE中,tan∠CED=2,∴二面角C-AB1-B的大小为arctan2
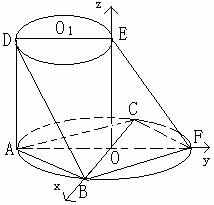
22.解:(Ⅰ)∵AD与两圆所在的平面均垂直,
∴AD⊥AB, AD⊥AF,故∠BAD是二面角B—AD—F的平面角,
依题意可知,ABCD是正方形,所以∠BAD=450.
即二面角B—AD—F的大小为450;
(Ⅱ)以O为原点,BC、AF、OE所在直线为坐标轴,建立空间直角坐标系(如图所示),则O(0,0,0),A(0,
,0),B(
,0,0),D(0,
,8),E(0,0,8),F(0,
,0)
所以,

设异面直线BD与EF所成角为
,则
直线BD与EF所成的角为

- ·上一篇:八年下册暑假园地答案
- ·下一篇:七年级数学《直线、射线、线段》同步测试题
《高一必修二《直线、平面、简单几何体》练习题》相关文章
- › 高一必修二《两条直线的平行与垂直》练习题
- › 高一必修二《直线的方程》练习题
- › 关于高一生物复习方法:高一必修复习提纲
- › 荆轲刺秦王(人教版高一必修)
- › 人教版高一必修4文言文阅读同步训练
- › 人教版高一必修一英语教案
- › 高一必修二《直线与方程》课堂练习
- › 高一必修二《圆与方程》课堂练习
- › 高一必修二《直线、平面、简单几何体》练习题
- › 高一必修一《直线与平面垂直的判定(一)》教案
- › 高一必修二《点到直线的距离》说课稿
- › 高一必修二《圆的标准方程》的说课稿
- › 北师大版高一必修二数学教案
- › 北师大版高一必修三数学教案
- › 牛津英语高一必修一教案
- › 高一必修一《圆的方程》教学设计
- 在百度中搜索相关文章:高一必修二《直线、平面、简单几何体》练习题
最新更新