高一数学《圆的标准方程》教学设计

标签：数学教学设计,http://www.manfen6.com 高一数学《圆的标准方程》教学设计,

　　

 

　　x+

　　

 

　　y=17 (教师板书)

　　师：对照圆的方程x2+y2=17和经过点P(

　　

 

　　，

　　

 

　　)的切线方程

　　

 

　　x+

　　

 

　　y=17，你能作出怎样的猜想?

　　生：。。。。。。

　　师：由x2+y2=17怎样写出切线方程

　　

 

　　x+

　　

 

　　y=17,与已知点P(

　　

 

　　，

　　

 

　　)有何关系?

　　(若看不出来，再看一例)

　　[例1/] 圆的方程是x2+y2=13，求过此圆上一点(2，3)的切线方程。

　　答案：2x+3y=13 即：2x+3y-13=0

　　师：发现规律了吗?(学生纷纷举手回答)

　　生：分别用切点的横坐标和纵坐标代替圆方程中的一个x和一个y，便得到了切线方程。

　　师：若将已知条件中圆半径改为r，点改为圆上任一点(xo,yo),则结论将会发生怎样的变化?大胆地猜一猜!

　　生：xox+yoy=r2.

　　师：这个猜想对不对?若对，可否给出证明?

　　生：。。。。。。

　　[例2]已知圆的方程是 x2+y2=r2，求经过圆上一点P(xo,yo)的切线的方程。

　　解：如图(上一页)，因为切线与过切点的半径垂直，故半径OP的斜率与切线的斜率互为负倒数

　　∵半径OP的斜率 K1=

　　

 

　　，∴切线的斜率 K=-

　　

 

　　=-

　　

 

　　∴所求切线方程：y-yo= -

　　

 

　　(x-xo)

　　即：xox+yoy=xo2+yo2 亦即：xox+yoy=r2. (教师板书)

　　当点P在坐标轴上时，可以验证上面方程同样适用。

　　归纳总结：圆的方程可看成 x.x+y.y=r2,将其中一个x、y用切点的坐标xo、yo 替换，可得到切线方程

　　[例3]右图为某圆拱桥的一孔圆拱的示意图.该圆拱跨度AB=20M，拱高OP=4M，在建造时每隔4M需用一个支柱支撑，求支柱A2P2的长度。(精确到0.01M)

　　引导学生分析，共同完成解答。

　　师生分析：①建系; ②设圆的标准方程(待定系数);③求系数(求出圆的标准方程);④利用方程求A2P2的长度。

　　

 

　　

 

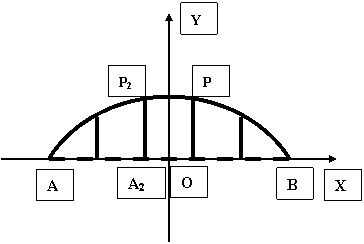
　　解：以AB所在直线为X轴，O为坐标原点，建立如图所示的坐标系。则圆心在Y轴上，设为

　　(0，b),半径为r，那么圆的方程是 x2+(y-b)2=r2.

　　∵P(0,4),B(10,0)都在圆上，于是得到方程组：

　　

 

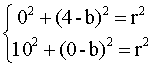
　　解得：b=-10.5 ,r2=14.52

　　∴圆的方程为 x2+(y+10.5)2=14.52.

　　将P2的横坐标x=-2代入圆的标准方程

　　且取y>0

　　得：y=

　　

 

　　≈14.36-10.5=3.86 (M)

　　答：支柱A2P2的长度约为3.86M。

　　Ⅳ.课堂练习、课时小结

　　课本P77练习2，3

　　师：通过本节学习，要求大家掌握圆的标准方程，理解并掌握切线方程的探求过程和方法，能运用圆的方程解决实际问题.

　　Ⅴ.问题延伸、课后作业

　　(一)若P(xo,yo)在圆(x-a)2+(y-b)2= r2上时，試求过P点的圆的切线方程。

　　课本P81习题7.7 : 1，2，3，4

　　(二)预习课本P77～P79

　　教学设计说明

　　设计思想：

　　在教学过程中，教师遵循数学发展规律，并依据建构主义教育理论，创设一系列数学实验环境，在情境中让学生观察、类比、猜想、尝试、探索、归纳并引导加以证明，强调主动建构，从深层次加强学生对知识的感知度，使学生能更好地理解和掌握圆的标准方程。

上一页  [1] [2] [3]  下一页

TAG: 教学  高一数学