高中数学《直线与平面的位置关系》练习题
11-01 11:57:02 | 浏览次数: 92618 次 | 栏目:数学知识点总结
标签:数学知识点总结,http://www.manfen6.com
高中数学《直线与平面的位置关系》练习题,
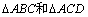






TAG: 练习题 高中数学 平面
或
; 15. MN||平面BDC; 16. 3cm; 17.
;
18. 连接AM,AN,并延长分别交BC,CD于点E,F,连接EF,由M,N分别是
的重心,得E,F分别是BC,CD的中点,则EF||BD,易证得BD||平面CMN;由
,得MN||EF,可证MN||平面ABD.
19. (1)由四边形EFGH是矩形可得,EF||GH,可证得EF||平面BCD,又因CD是过EF的平面ACD与平面BCD的交线,则EF||CD,所以CD||平面EFGH.
(2)由CD||平面EFGH,可证得CD||GH;同理可证AB||GF;
FGH就是异面直线AB,CD所成的角(或补角),因为EFGH是矩形,所以
FGH=900,则异面直线AB,CD所成的角为900.
20. 证明:(1)

AC||平面MNP,

BD||平面MNP.
(2)
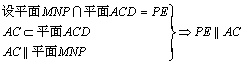
,即平面MNP与平面ACD的交线||AC.
21. 再找一条与B1H垂直的直线AC,证AC
平面BB1D1D即可,又AC?OD1=O, 因此 B1H
平面AD1C.
- ·上一篇:七年级数学《正数和负数》同步测试题
- ·下一篇:2016年五年级数学下册暑假作业题及答案 (彩色版)
《高中数学《直线与平面的位置关系》练习题》相关文章
- › 高中数学集合与函数公式定理记忆口诀
- › 高中数学公式汇总
- › 高中数学三角函数公式定理记忆口诀
- › 了解高中数学特点是高一数学学习关键
- › 高中数学与初中数学有哪些变化
- › 高一同学必读:如何学好高中数学 ?
- › 北京四中名师指点:从高一开始学好高中数学
- › 高一新生篇:如何学好高中数学
- › 高中数学笔记误区分析
- › 高中数学学习方法指导
- › 影响高中数学成绩的原因及解决方法
- › 高中数学第一轮复习建议
- › 高中数学公式大全
- › 怎样学好高中数学-学好高中数学的几个技巧
- › 高中数学教学总结与反思
- › 浅谈影响高中数学成绩的原因
- 在百度中搜索相关文章:高中数学《直线与平面的位置关系》练习题
最新更新