高中数学必修一《函数的单调性》教学设计

标签：数学教学设计,http://www.manfen6.com 高中数学必修一《函数的单调性》教学设计,

 

　　的图象,能说出这个函数分别在哪个区间为增函数和减函数吗?

　　

 

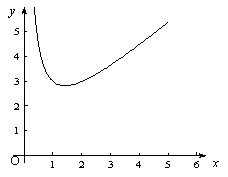
　　学生的困难是难以确定分界点的确切位置.

　　通过讨论，使学生感受到用函数图象判断函数单调性虽然比较直观，但有时不够精确，需要结合解析式进行严密化、精确化的研究.

　　〖设计意图〗使学生体会到用数量大小关系严格表述函数单调性的必要性.

　　问题2：如何从解析式的角度说明

　　

 

　　在

　　

 

　　为增函数?

　　预案： (1) 在给定区间内取两个数，例如1和2，因为12<22,所以

　　

 

　　在

　　

 

　　为增函数.

　　(2) 仿(1)，取很多组验证均满足，所以

　　

 

　　在

　　

 

　　为增函数.

　　(3) 任取

　　

 

　　,因为

　　

 

　　,即

　　

 

　　，所以

　　

 

　　在

　　

 

　　为增函数.

　　对于学生错误的回答，引导学生分别用图形语言和文字语言进行辨析,使学生认识到问题的根源在于自变量不可能被穷举，从而引导学生在给定的区间内任意取两个自变量

　　

 

　　.

　　〖设计意图〗把对单调性的认识由感性上升到理性认识的高度,完成对概念的第二次认识.事实上也给出了证明单调性的方法，为证明单调性做好铺垫.

　　3.抽象思维，形成概念

　　问题：你能用准确的数学符号语言表述出增函数的定义吗?

　　师生共同探究，得出增函数严格的定义，然后学生类比得出减函数的定义.

　　(1)板书定义

　　(2)巩固概念

　　判断题：

　　①

　　

 

　　.

　　②若函数

　　

 

　　.

　　③若函数

　　

 

　　在区间

　　

 

　　和(2,3)上均为增函数，则函数

　　

 

　　在区间(1,3)上为增函数.

　　④因为函数

　　

 

　　在区间

　　

 

　　上都是减函数，所以

　　

 

上一页  [1] [2] [3] [4]  下一页

TAG: 教学  高中数学  单调性