七年级下册《多边形的内角和》教学案例
11-01 11:56:30 | 浏览次数: 19418 次 | 栏目：数学教学设计
标签：数学教学设计,http://www.manfen6.com
七年级下册《多边形的内角和》教学案例,
TAG: 教学
师质疑：三角形的内角和是
(出示教师用的教具──三角板)，四边形的内角和是多少度?
生思考
师提示：长方形的每个内角都是多少度?正方形的每个内角呢?看看我们的书、本、桌面。
师：请同学们猜想一般四边形内角和的度数。
生答：四边形内角和是
.(教师板书)
师肯定：同学们回答的非常好!我们小学学过的长方形的内角和是
，正方形的内角和也是
，由此我们猜测一般四边形内角和也是
。
师指出：这个结论是否正确呢?我们要从理论上加以验证。
点评 以小学学过长方形、正方形的每个内角都是
为依托，猜想一般四边形内角和的度数。向学生渗透由具体到抽象、由特殊到一般的数学思想方法。
2、探索研究解释的方法，并交流不同方法
师质疑：怎样说明四边形内角和是
呢?
师指出：处理复杂问题普遍实用的方法，就是把未知转化为已知，用已有知识研究新问题。所以，研究四边形的问题可转化为已学过的知识去解决。
生答：三角形。
师：对!同学们回答的非常好!把四边形问题转化为三角形知识解决。
师追问：转化的关键?
生答：作辅助线。
点评 研究四边形的问题可转化为三角形知识去解决，向学生渗透“化归”的数学思想方法。
师：请同学们考虑说明的方法。
生独立思考──生生交流讨论(教师个别辅导)──生再独立思考。
师：请同学们说说各自的思路。
众生：如图4，连接AC……如图5，在BC边上任取一点P(也可在AB或CD或AD边上任取一点P)，连接AP，DP……如图6，在四边形ABCD内任取一点O，连接AO，BO，CO，DO……如图7，在四边形ABCD外任取一点P，连接AP，BP，CP，DP……如图8，过D点作AB平行DP，交BC于P点……
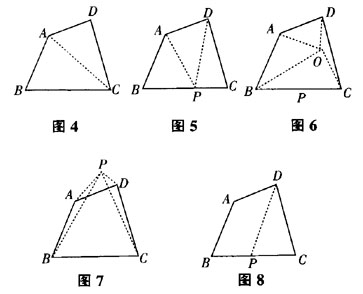
师：同学们的思路都非常的好!你想到的是哪一种方法呢?
生：比较而言，应该说连接AC时说明的过程最好。
点评 四边形内角和这一结论的解释说明是本节课的一个重点，添加辅助线是关键。本环节的学习中，探索了多种的说明方法，活跃了学生的思维。在教学过程中，应鼓励学生通过独立思考，不拘一格，创造性地解决问题，使学习数学成为再发现和再创造的过程。
3、归纳概括所得结论
师指出：经过分析，同学们猜想得到的结论“四边形的内角和等于
”是正确的。这是这节课我们学习的一个重点内容──四边形的内角和等于
.
师强调：同学们要熟记这个内容，并能运用它解决有关的问题。
师指出：同学们还要体会得到“四边形内角和是
”的方法。即通过作辅助线将四边形问题转化为三角形知识解决。这种解决问题的方法在今后的解题中经常会用到。
师继续指出：从分析思路看，同学们得到了多种方法，各种方法都非常好。那么，当一个题目有多种方法时，特别是几何问题，往往都有多种方法，通常我们选择最简单的方法。
点评 (1)从特殊四边形(长方形、矩形)中观察、分析、猜测、验证获取新知(内角和是
)。(2)从已有知识结构中讨论分析归纳获得新的创新。引导学生进人一种研究状态，获得的新知对学生来说，就是一种创新。
4、巩固性应用
师：请同学们解答下面的判断题
(1)四边形的各内角可以都是锐角。( )
变式1：将“锐角”改为“直角”。
变式2：将“锐角”改为“钝角”。
生口答：(l)错误。变式1正确。变式2错误。
(2)在一个四边形中，如果有两个角都是直角，那么其余的两个角的关系一定是互为补角。( )
生口答：正确。
(3)如图9，四边形ABCD中，
的大小不能确定。( )
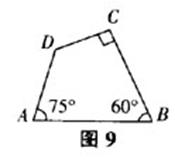
生口答：错误。
- ·上一篇：七年级数学《平行线的性质》教学设计
- ·下一篇：八年级下册数学《平行四边形》教学设计
《七年级下册《多边形的内角和》教学案例》相关文章
- › 七年级下册语文暑假作业歇后语
- › 黄河颂教案下载(人教版七年级下册语文)
- › 诗两首课件下载(人教版七年级下册语文)
- › 伤仲永教案下载(人教版七年级下册语文)
- › 2016年初中七年级下册数学练习卷
- › 2016年七年级下册数学模拟练习题及答案
- › 2016年七年级下册英语暑假作业答案
- › 艰难的国运与雄健的国民课件下载(人教版七年级下册语文)
- › 人教版七年级下册语文期末试卷及答案
- › 人教版七年级下册期末数学测评卷
- › 人教版七年级下册数学期末试卷
- › 人教版数学七年级下册期末总复习题
- › 人教版数学七年级下册-知识点整理
- › 人教七年级下册数学期末模拟卷2
- › 人教版七年级下册（初一下）语文：《诗两首》教案（3篇）
- › 人教版七年级下册（初一下）语文：《口技》教案
- 在百度中搜索相关文章：七年级下册《多边形的内角和》教学案例
最新更新