高中数学《 平面向量的基本定理及坐标表示》同步练习题
11-01 11:53:31 | 浏览次数: 39118 次 | 栏目：数学知识点总结
标签：数学知识点总结,http://www.manfen6.com
高中数学《 平面向量的基本定理及坐标表示》同步练习题,
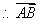
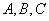
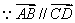
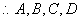
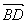
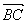
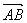
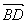
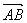
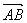
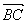
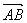
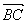
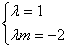
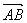TAG: 练习题 高中数学 平面
不平行，此时
不在一条直线上;
当
时，
，
//
，此时
三点共线.
又
，
四点在一条直线上.
综上 当
时，
四点在一条直线上.
当堂练习：
1.B; 2.B; 3.A; 4.B; 5.D; 6.A; 7. -4; 8. 3
; 9. -3，15; 10. (8,-4);
11.解析：(1)
=
+
=2e1-8e2+3(e1+e2)=5e1-5e2=5
∴
与
共线
又直线BD与AB有公共点B， ∴A、B、D三点共线
(2)∵λe1-e2与e1-λe2共线
∴存在实数k，使λe1-e2=k(e1-λe2)，化简得(λ-k)e1+(kλ-1)e2=0
∵e1、e2不共线， ∴由平面向量的基本定理可知：λ-k=0且kλ-1=0
解得λ=±1，故λ=±1.
12.解法一：∵A、B、C三点共线即
、
共线
∴存在实数λ使得
=λ
即i-2j=λ(i+mj)
于是
∴m=-2 即m=-2时，A、B、C三点共线.
解法二：依题意知：i=(1,0),j=(0,1)
则
- ·上一篇：“曹冲称象” VS “等量代换”=思维
- ·下一篇：航天惨剧
《高中数学《 平面向量的基本定理及坐标表示》同步练习题》相关文章
- › 高中数学集合与函数公式定理记忆口诀
- › 高中数学公式汇总
- › 高中数学三角函数公式定理记忆口诀
- › 了解高中数学特点是高一数学学习关键
- › 高中数学与初中数学有哪些变化
- › 高一同学必读：如何学好高中数学 ？
- › 北京四中名师指点：从高一开始学好高中数学
- › 高一新生篇：如何学好高中数学
- › 高中数学笔记误区分析
- › 高中数学学习方法指导
- › 影响高中数学成绩的原因及解决方法
- › 高中数学第一轮复习建议
- › 高中数学公式大全
- › 怎样学好高中数学-学好高中数学的几个技巧
- › 高中数学教学总结与反思
- › 浅谈影响高中数学成绩的原因
- 在百度中搜索相关文章：高中数学《 平面向量的基本定理及坐标表示》同步练习题
最新更新