高中数学《一次函数》练习题

11-01 11:57:02 | 浏览次数: 14418 次 | 栏目：数学知识点总结

标签：数学知识点总结,http://www.manfen6.com 高中数学《一次函数》练习题,

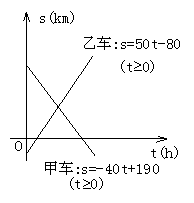
　　(1)就这两个一次函数图像所反映的两汽车在这条公路上行驶的状况填写如下的表格.

　　行驶方向速度的大小(km)h出发前的位置

　　甲车

　　乙车

　　(2)甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.

　　参考答案：

　　1.B 2.A 3.D 4.C

　　5.y =0.15x+24,98,33.3 6.①

　　,亏损 ②3 ③y1=

　　x ④y=

　　x—2

　　7.(1)超过3000千米，(2)3000千米(3)个体

　　8.(1)

　　(2)当a≤—1时，S=2;当—1

　　或

　　10.(1)设直线L1的解析式为y1=k1x+2,由图像得17=500k1+2,解得k1=0.03.

　　∴y1=0.03x+2(0≤x≤2 000).

　　设直线L2的解析式为y2=k2x+20,

　　由图像得26=500k2+20,解得k2=0.012,

　　y=0.012x+20(0≤x≤2 000).

　　(2)当y1=y2时,两种灯的费用相等.

　　0.03x+2=0.012x+20,解得x=1 000.

　　∴当照明时间为1 000小时时,两种灯的费用相等.

　　(3)节能灯使用2 000小时,白炽灯使用500小时.

　　11.解:(1)甲车:x轴负方向(向左),40,零千米路标右侧190千米;

　　乙车:x轴正方向(向右),50,零千米路标左侧80千米处.

　　(2)甲乙两车相遇

　　设经过t小时两车相遇,由

　　得

　　所以经过3小时两车相遇,相遇在零千米路标右侧70千米处.