游戏学数学 数图形

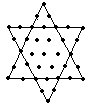
想：直接数点子太难，可把这个六角星形的图形分解为一个大平行四边形和四个小三角形（如右图），就很容易数出点子的个数。

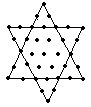
解：大平行四边形中点子的个数：

5×5＝25（个）

四个小三角形点子的个数：

3×4＝12（个）

点子的总个数：

25＋12＝37（个）

答：共有37个点子。

2.下图是一个正方形钉子板的示意图，16个黑点子表示16颗钉子，以这些点为顶点，用皮筋围正方形，一共可以围成多少个大大小小的正方形？

想：先按数线段的方法，用边长所含最短线段的几种情况，算出正正当当放置的正方形个数。再数斜着围成的正方形个数。

解：平正放置的正方形个数：

9＋4＋1＝14（个）

倾斜放置的正方形个数：

4＋2＝6（个）

一共含有正方形个数：

14＋6＝20（个）

答：一共可以围成大大小小20个正方形。

3.图中有几种几何图形？各有多少个？

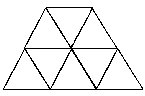
想：先分清有几种几何图形，再按基本的数图形的方法数出各自的个数。

解：图中有三角形，平行四边形和梯形。

三角形个数：

平行四边形个数：

两个三角形组成平行四边形个数十四个小三角形组成的平行四边形个数＝10＋4＝14（个）

梯形的个数：

4.下图中含有☆的长方形有多少个？

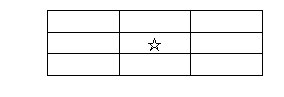
想：为了不重复不遗漏，可由小到大，由内向外数。

合起来是4＋3＋4＋4＋1＝16（个）。

答：符合条件的长方形有16个。

5.右图是由九个边长为1厘米的小正方形组成的大正方形。

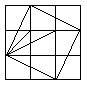
（1）图中面积为1/2平方厘米的三角形有几个？

（2）图中面积为1平方厘米的三角形有几个？

想：利用等底等高面积相等的道理，分类进行观察。

解：面积为1/2平方厘米的三角形有4个。

面积为1平方厘米的三角形有10个。

6.下图，BC与AD平行，BD与AE平行，AB与EC平行。找出与三角形ABC面积相等的三角形？

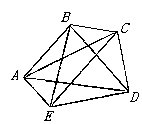
想：找与三角形ABC面积相等的三角形，也就是找与三角形ABC等底等高的三角形。为了解决好这个问题，应充分利用三组平行线的条件找高。

答：三角形BDC、AEB、AED与三角形ABC面积相等。

7.下图中，大正方形是由9个面积相等的小正方形组成。以不在同一直线上的三个顶点组成三角形，这些三角形中有多少个与阴影三角形面积相等？

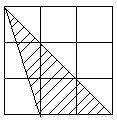
想：找与阴影面积相等的三角形，实际就是找与它等底等高的三角形。为了方便，可分不同类型进行研究。

（1）边长是2，高是3的三角形个数：

4×2×4＝32（个）

（2）边长是3，高是2，与（1）重复的不计入，个数是：

8×2＝16（个）

合起来是：32＋16＝48（个）

答：有48个三角形与阴影三角形面积相等。

8.下图是一个棋盘，将一个白子和一个黑子放在棋盘线交叉点上，但不能在同一条棋盘线上，共有多少种不同的放法？

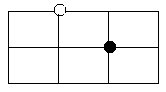
想：黑子确定一个位置，白子就有6个不同的放法。而黑子总共有12个不同的位置，由此，便可推算出一共的放法。

解：12×6＝72（种）

答：共有72种不同的放法。

9.下图中有多少个长方形？多少个正方形？多少个三角形？

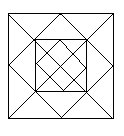
想：由外向里，从第二个和第四个正方形中数长方形个数。仍从第二和第四个正方形中数正方形个数，并加上四层的正方形。由内两层正方形和外两层正方形数三角形个数，再加上二、三两层正方形形成的三角形个数。

解：长方形个数：4＋4＝8（个）

正方形个数：4＋4＋4＝12（个）

三角形个数：20＋20＋4＝44（个）

答：有 8个长方形，12个正方形，44个三角形。