高考第二轮复习数学学案解三角形（1）
11-01 12:03:33 | 浏览次数: 53818 次 | 栏目：高考数学复习方法
标签：高考数学复习方法,http://www.manfen6.com
高考第二轮复习数学学案解三角形（1）,
一、学法导航 处理三角形问题，必须结合三角形全等的判定定理理解斜三角形的四类基本可解型，特别要多角度（几何作图，三角函数定义，正、余弦定理，勾股定理等角度）去理解“边边角”型问题可能有两解、一解、无解的三种情况，根据已知条件判断解的情况，并能正确求解. 1.三角形中的边角关系 三角形内角和等于180°； 三角形中任意两边之和大小第三边，任意两边之差小于第三边； 三角形中大边对大角，小边对小角； 正弦定理中,a=2R·sinA,b=2R·sinB,c=2R·sinC，其中R是△ABC外接圆半径. 在余弦定理中:2bccosA=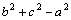
.
三角形的面积公式有:S=
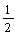ah,S=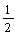absinC,S=
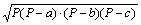其中，h是BC边上高，P是半周长.
2.利用正、余弦定理及三角形面积公式等解任意三角形
已知两角及一边，求其它边角，常选用正弦定理.
已知两边及其中一边的对角，求另一边的对角，常选用正弦定理.
已知三边，求三个角，常选用余弦定理.
已知两边和它们的夹角，求第三边和其他两个角，常选用余弦定理.
已知两边和其中一边的对角，求第三边和其他两个角，常选用正弦定理.
3.利用正、余弦定理判断三角形的形状
常用方法是：①化边为角；②化角为边.
4.解斜三角形在实际中的运用高考资源网
5．三角形的面积公式：
（1）△＝
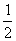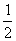aha＝bhb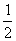＝chc（ha、hb、hc分别表示a、b、c上的高）；
（2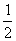）△＝absinC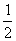＝bcsinA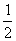＝acsinB；
（3）△＝
＝
＝
；
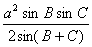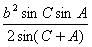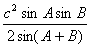（4）△＝2R2sinAsinBsinC.（R为外接圆半径）
（5）△＝
；
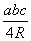（6）△＝
；
；
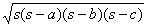（7）△＝r·s.
6.三角形中的三角变换
三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点.
（1）角的变换
因为在△ABC中，A+B+C=π，所以sin(A+B)=sinC；cos(A+B)=－cosC；tan(A+B)=－tanC.
TAG: 数学 三角形
一、学法导航 处理三角形问题，必须结合三角形全等的判定定理理解斜三角形的四类基本可解型，特别要多角度（几何作图，三角函数定义，正、余弦定理，勾股定理等角度）去理解“边边角”型问题可能有两解、一解、无解的三种情况，根据已知条件判断解的情况，并能正确求解. 1.三角形中的边角关系 三角形内角和等于180°； 三角形中任意两边之和大小第三边，任意两边之差小于第三边； 三角形中大边对大角，小边对小角； 正弦定理中,a=2R·sinA,b=2R·sinB,c=2R·sinC，其中R是△ABC外接圆半径. 在余弦定理中:2bccosA=
.
三角形的面积公式有:S=ah,S=absinC,S=其中，h是BC边上高，P是半周长.
2.利用正、余弦定理及三角形面积公式等解任意三角形
已知两角及一边，求其它边角，常选用正弦定理.
已知两边及其中一边的对角，求另一边的对角，常选用正弦定理.
已知三边，求三个角，常选用余弦定理.
已知两边和它们的夹角，求第三边和其他两个角，常选用余弦定理.
已知两边和其中一边的对角，求第三边和其他两个角，常选用正弦定理.
3.利用正、余弦定理判断三角形的形状
常用方法是：①化边为角；②化角为边.
4.解斜三角形在实际中的运用高考资源网
5．三角形的面积公式：
（1）△＝aha＝bhb＝chc（ha、hb、hc分别表示a、b、c上的高）；
（2）△＝absinC＝bcsinA＝acsinB；
（3）△＝＝＝；
（4）△＝2R2sinAsinBsinC.（R为外接圆半径）
（5）△＝；
（6）△＝；；
（7）△＝r·s.
6.三角形中的三角变换
三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点.
（1）角的变换
因为在△ABC中，A+B+C=π，所以sin(A+B)=sinC；cos(A+B)=－cosC；tan(A+B)=－tanC.
- ·上一篇：常用的开发右脑的几种方式
- ·下一篇：2011高考全国卷数学（文科）试题答案
《高考第二轮复习数学学案解三角形（1）》相关文章
- › 高考第二轮复习数学学案解三角形（1）
- › 高考第二轮复习数学学案解三角形（2）
- 在百度中搜索相关文章：高考第二轮复习数学学案解三角形（1）
最新更新